Proportional Apportionment

Calculate seat apportionment for legislative bodies with various methods. These methods include divisor methods (e.g. D’Hondt, Webster or Adams), largest remainder methods and biproportional apportionment.

Mit diesem R-Package können mittels verschiedener Sitzzuteilungsverfahren Wählerstimmen in Abgeordnetensitze umgerechnet werden. Das Package beinhaltet Quoten-, Divisor- und biproportionale Verfahren (Doppelproporz oder “Doppelter Pukelsheim”).

Installation

Install the package from CRAN:

install.packages("proporz")

Alternatively, install the development version from Github:

# install.packages("remotes")
remotes::install_github("polettif/proporz")

Apportionment methods overview

proporz() distributes seats proportionally for a vector of votes according to the following methods:

Divisor methods (Wikipedia)
- D’Hondt, Jefferson, Hagenbach-Bischoff
- Sainte-Laguë, Webster
- Adams
- Dean
- Huntington-Hill
Largest remainder method (Wikipedia)
- Hare-Niemeyer, Hamilton, Vinton

library(proporz)
votes = c("Party A" = 651, "Party B" = 349, "Party C" = 50)

proporz(votes, n_seats = 10, method = "sainte-lague")
#> Party A Party B Party C 
#>       7       3       0

proporz(votes, 10, "huntington-hill", quorum = 0.05)
#> Party A Party B Party C 
#>       6       4       0

Biproportional Apportionment

Biproportional apportionment (Wikipedia) is a method to proportionally allocate seats among parties and districts.

We can use the provided uri2020 data set to illustrate biproportional apportionment with biproporz(). You need a ‘votes matrix’ as input which shows the number of votes for each party (rows) and district (columns). You also need to define the number of seats per district.

(votes_matrix <- uri2020$votes_matrix)
#>      Altdorf Bürglen Erstfeld Schattdorf
#> CVP    11471    2822     2309       4794
#> SPGB   11908    1606     1705       2600
#> FDP     9213    1567      946       2961
#> SVP     7756    2945     1573       3498

(district_seats <- uri2020$seats_vector)
#>    Altdorf    Bürglen   Erstfeld Schattdorf 
#>         15          7          6          9

biproporz(votes_matrix, district_seats)
#>      Altdorf Bürglen Erstfeld Schattdorf
#> CVP        5       2        2          3
#> SPGB       4       1        2          2
#> FDP        3       1        1          2
#> SVP        3       3        1          2

You can use pukelsheim() for dataframes in long format as input data. It is a wrapper for biproporz(). zug2018 shows an actual election result for the Canton of Zug in a dataframe. We use this data set to create input data for pukelsheim(). The other parameters are set to reflect the actual election system.

# In this data set, parties are called 'lists' and districts 'entities'.
votes_df = unique(zug2018[c("list_id", "entity_id", "list_votes")])
district_seats_df = unique(zug2018[c("entity_id", "election_mandates")])

seats_df = pukelsheim(votes_df,
                      district_seats_df,
                      quorum = quorum_any(any_district = 0.05, total = 0.03),
                      winner_take_one = TRUE)

head(seats_df)
#>   list_id entity_id list_votes seats
#> 1       2      1701       8108     2
#> 2       1      1701       2993     0
#> 3       3      1701      19389     3
#> 4       4      1701      14814     2
#> 5       5      1701       4486     1
#> 6       6      1701      15695     3

The apportionment scenarios vignette contains more examples.

Shiny app

The package provides a basic Shiny app where you can calculate biproportional apportionment on an interactive dashboard. You need to have the packages shiny and shinyMatrix installed.

# install.packages("shiny")
# install.packages("shinyMatrix")
proporz::run_app()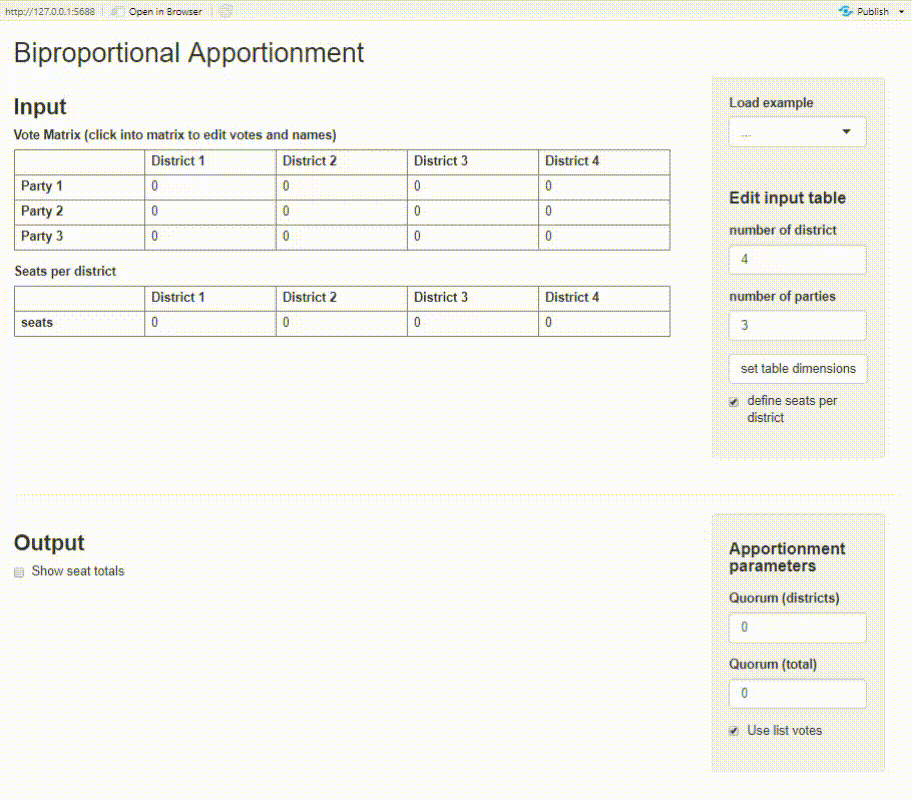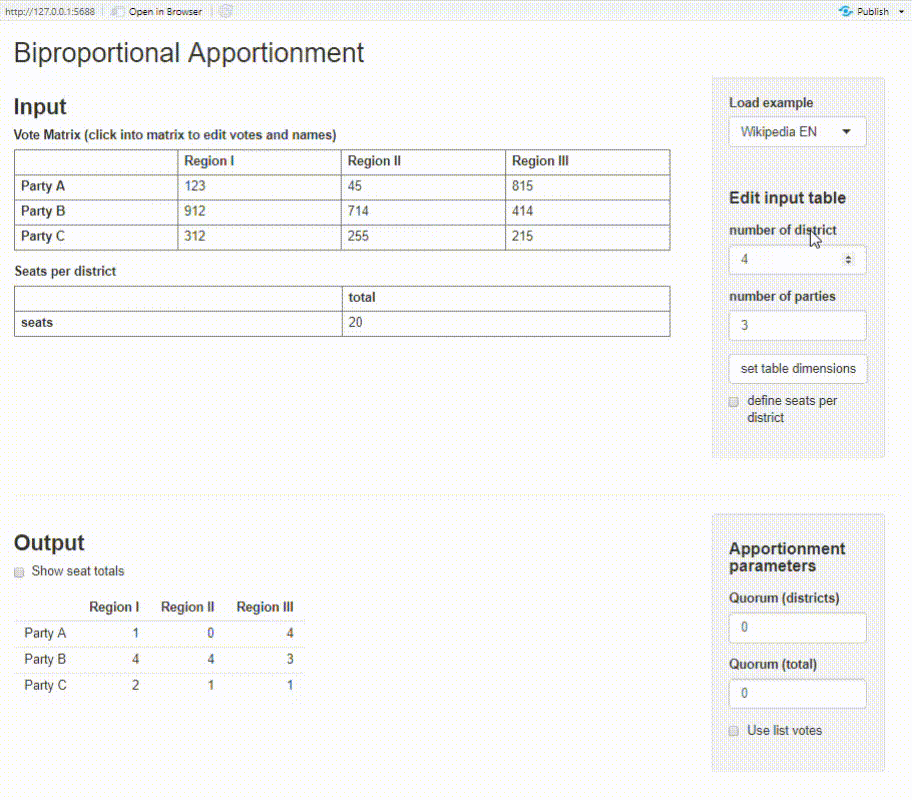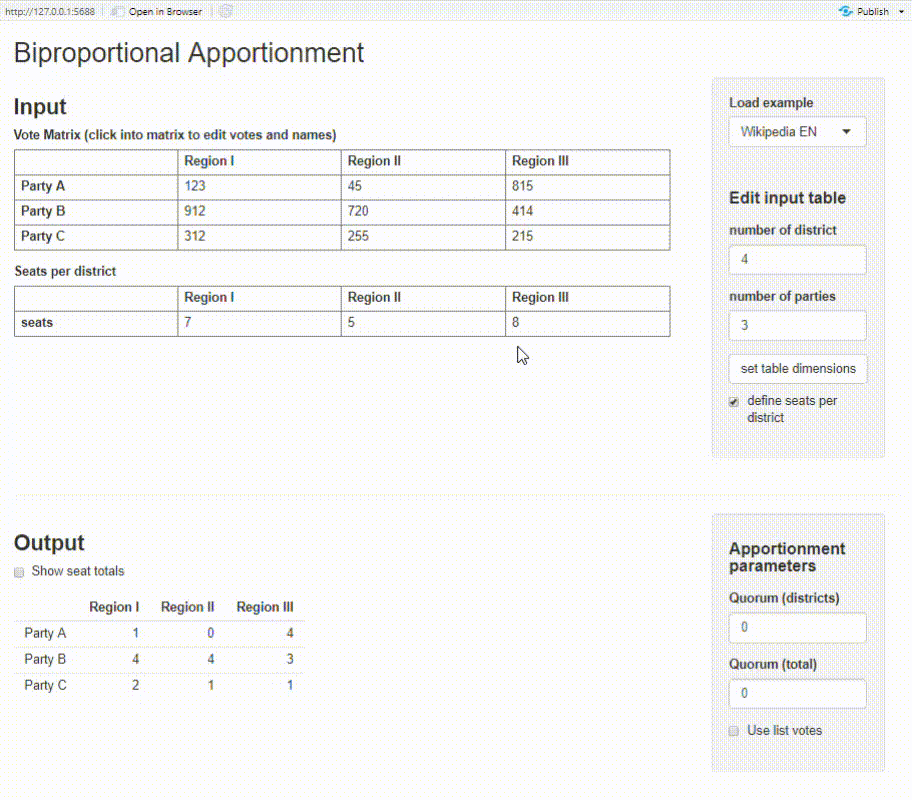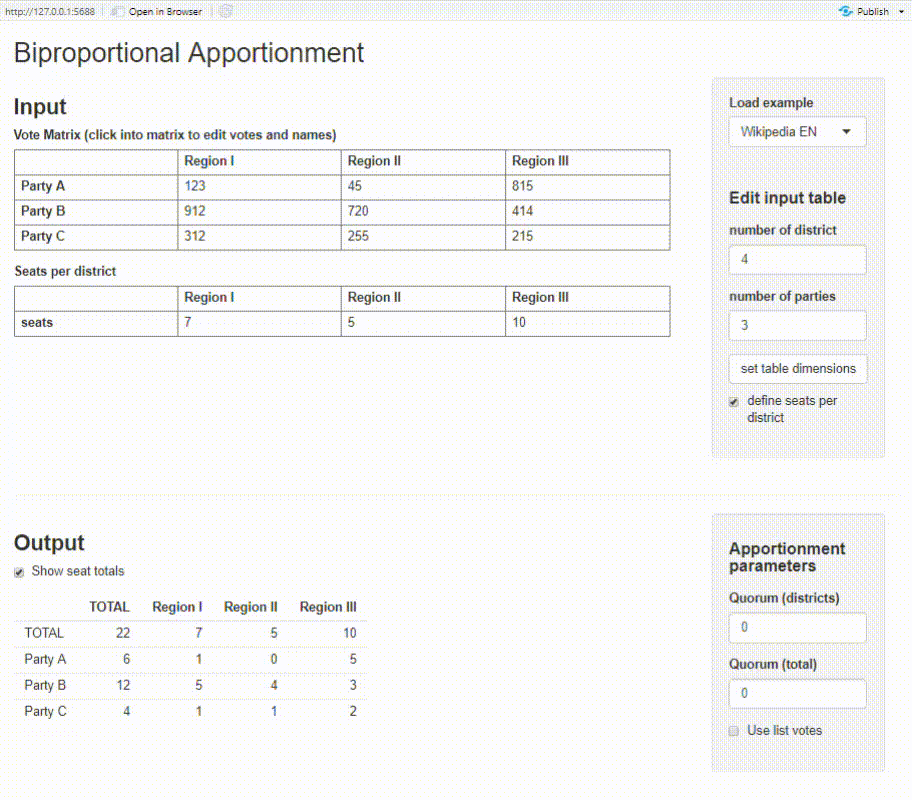

Function details

Full function reference

Divisor methods

You can use divisor methods directly:

votes = c("Party A" = 690, "Party B" = 370, "Party C" = 210, "Party D" = 10)

# D'Hondt, Jefferson or Hagenbach-Bischoff method
divisor_floor(votes, 10)
#> Party A Party B Party C Party D 
#>       6       3       1       0

# Sainte-Laguë or Webster method
divisor_round(votes, 10)
#> Party A Party B Party C Party D 
#>       5       3       2       0

# Adams method
divisor_ceiling(votes, 10)
#> Party A Party B Party C Party D 
#>       4       3       2       1

# Dean method
divisor_harmonic(votes, 10)
#> Party A Party B Party C Party D 
#>       5       2       2       1

# Huntington-Hill method
divisor_geometric(votes, 10)
#> Party A Party B Party C Party D 
#>       5       3       1       1

Largest remainder method

The largest remainder method is also accessible directly:

votes = c("I" = 16200, "II" = 47000, "III" = 12700)

# Hamilton, Hare-Niemeyer or Vinton method
largest_remainder_method(votes, 20)
#>   I  II III 
#>   4  13   3

proporz

Installation

Apportionment methods overview